Komplexní integrace
|
|
Problém:
Jak se v komplexní rovině chodí po schodech?
Řešení:
Zkusíme integrovat funkci 1/z. Vzhledem k tomu, že exponenciála má za derivaci opět exponenciálu, bude primitivní funkcí k 1/z v komplexní rovině komplexní logaritmus.
Takže pokud se bude integrovat podle jednotkové kružnice proti směru hodinových ručiček,
budeme hodnoty primitivní funkce odečítat na následujícím obrázku a zjistíme,
že si logaritmus při tom nasbíral přírůstek 2.pi.i.
Když ale budeme hledat tentýž přírůstek na reálné a imaginární složce komplexního logaritmu zvlášť,
dostaneme se na schody.
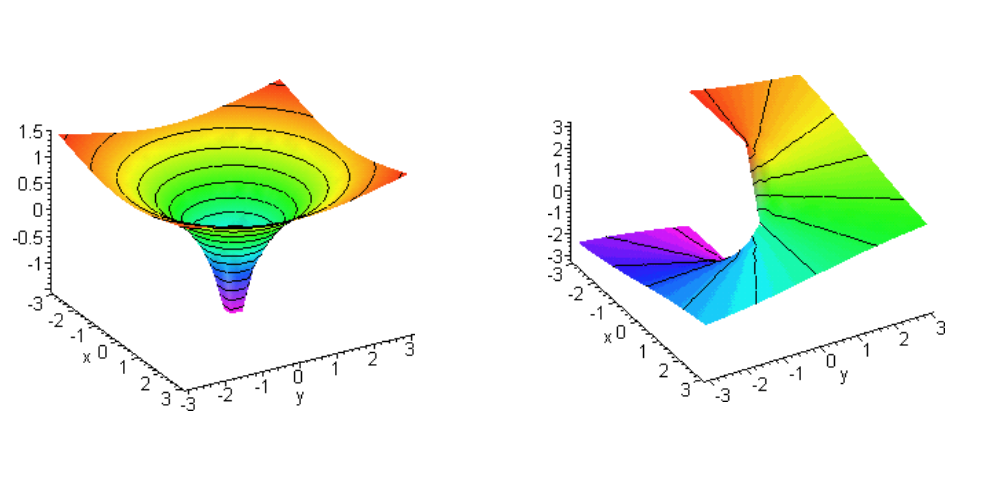
A takhle se to při integrování prostě chodí po schodech.