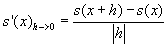
Derivace součinu funkcí
Derivace součinu funkcí
Nechť funkce s je spojitá v bodě x. Její derivaci v bodě x lze vyjádřit jako:
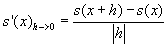
Derivace součinu funkcí f a g v bodě x, lze vyjádřit jako:
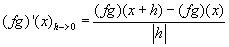
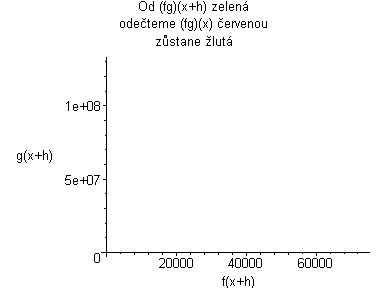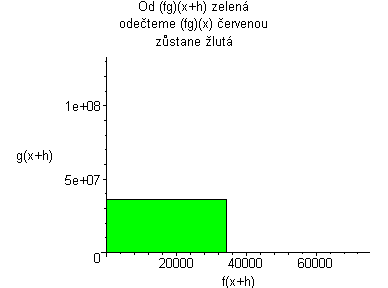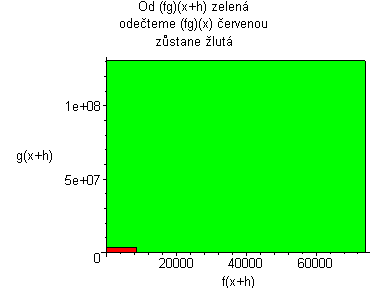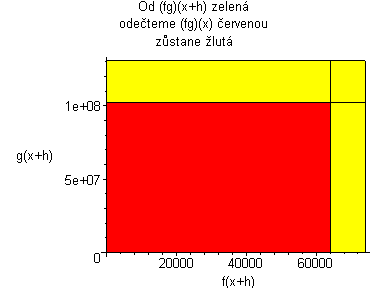
|
Kde: zelená plocha znázorňuje (fg)(x+h) červená plocha znázorňuje (fg)(x) Když červenou odečteme od zelené, tak zůstane žlutá plocha. žlutá:= f(x)(g(x+h)-g(x))+g(x)(f(x+h)-f(x))+((f(x+h)-f(x))(g(x+h)-g(x))) Když dosadíme do vzorce, tak žlutá plocha lze vyjádřit jako: 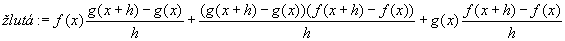
|
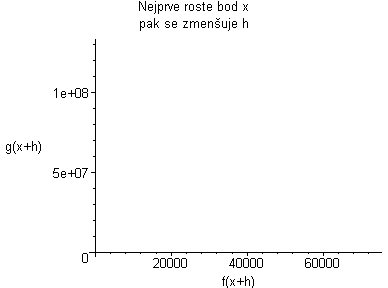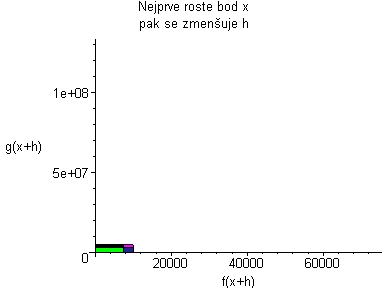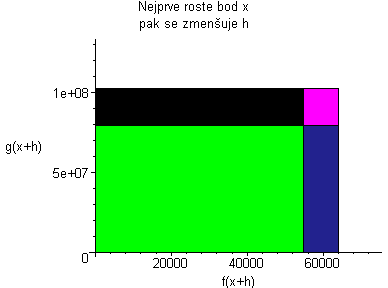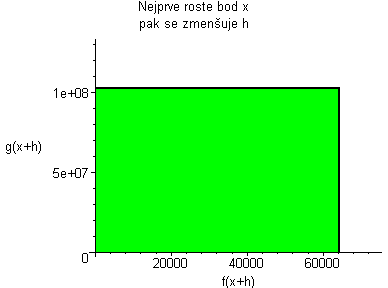
|
Plochu (fg)(x+h) animujeme podle rostoucího x, a pak se díváme co se děje s grafem, když h se blíží k nule. Po dosazení do vzorce dostaneme vztahy: 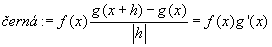 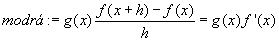 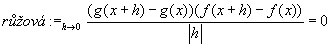 Pro h jdoucí k nule dostaneme tedy vzorec pro derivaci součinu: 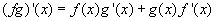
|
 |
 |
 |
 |
| Pro zajímavost: Součin funcí a derivace Srovnání grafů Součinu derivací a Derivace součinu. |
|
![[Maple Plot]](images/spojitost53.gif) |
![[Maple Plot]](images/spojitost57.gif) |
![[Maple Plot]](images/spojitost56.gif) |
![[Maple Plot]](images/spojitost58.gif) |
![[Maple Plot]](images/spojitost55.gif) |
![[Maple Plot]](images/spojitost61.gif) |