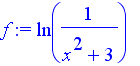
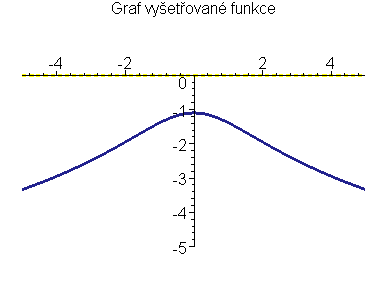
Pro x -> (+5)- má limita hodnotu -2 ln(2)-ln(7).
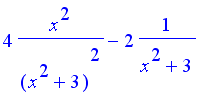
| Funkce f(x)=ln(1/(x2+3)) | ||
| Spojitost | Funkce je spojitá na celém definičním oboru. Vyšetřuji ji na intervalu (-5;5). | 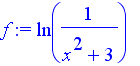  |
| Průsečíky se souřadnými osami | Y[0;-ln(3)] | |
| Symetrie | Funkce je sudá. | |
| Limity | Pro x -> (-5)+ má limita hodnotu -2 ln(2)-ln(7). Pro x -> (+5)- má limita hodnotu -2 ln(2)-ln(7). |
|
| První derivace | f'(x)=-2x/(x2+3) je všude spojitá | |
| Extrémy a monotonie | V bodě M[0;-ln(3)] je lokální maximum. Na (-5,0) funkce roste. Na (0,5) funkce klesá. | |
| Druhá derivace | f''(x)=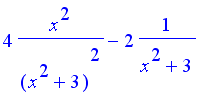 |
|
| Konvexita, konkávita, inflexní body | Inflexní body mají souřadnice [± |
|
| Obor hodnot | Funkce na svém definičním oboru (tj. na (-5;5) ) nabývá funkčních hodnot z intervalu (-ln(28); -ln(3)). | |
| Asymptoty | Funkce nemá v ±nekonečnu asymptotu. | |
| Předchozí | Zpět na úvod... | Následující |